Při triangulaci množiny bodů, je žádoucí aby vytvořené trojúhelníky byly co nejvíce rovnostranné. Pokud to takto provedeme, každý trojúhelník by měl co nejlépe lokálně reprezentovat hodnotu povrchu. Další požadovaná charakteristika triangulačního procesu je, aby byla produkována jednoznačná triangulace nezávisle na počátečním bodě nebo orientaci množiny dat. Tyto výsledky budou předpověditelné a jednoduše opakovatelné. Sibson (1978) ukázal, že Dalaunayho triangulace tyto podmínky obecně splňuje, i přes to, že jsou určité konfigurace množiny dat (jako např. pravoúhlý GRID) která má na výstupu lokálně nejednoznačné řešení.
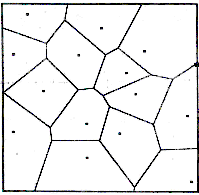
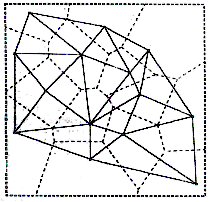
Delaunayho triangulace je blízce příbuzná k Dirichletově mozaikování (Dirichlet tessellation) množiny bodů, které rozdělí body unikátní množinou polygonů, které se nazývají Thiessenovy polygony, nebo také Voroniovy diagramy. Thiesenovy polygony ohradí všechny body oblastí, ve které jsou všechny místa bližší k danému bodu než k jinému bodu z dané množiny bodů. Viz. obr. 1. Každá hrana každého polygonu je kolmá osa oddělující ohrazený bod od sousedních bodů sousedním polygonem. Když jsou všechny sousední body propojeny hranami, Delaunayho triangulace končí. Viz. obr. 2. Zjednodušený popis algoritmu: Algoritmus vezme tři body, proloží jimi kružnici, když uvnitř kružnice neleží bod, vytvoří trojúhelník, pokud tam bod je, vybere jiné tři body.
Představme si danou množinu P obsahující n bodů v rovině, každý s hodnotou souřadnice Z. K převedení této informace do TINu bychom mohli jednoduše provést triangulaci této množiny bodů. Triangulace je vlastně interpolace oblasti založená na bodech P. Běžně se používá Delaunayho triangulace, protože vytváří dobře tvarované trojúhelníky. Již delší dobu jsou známy efektivní algoritmy Delaunayho triangulace.
Pokud interpolace pomocí Delaunayho triangulace není vhodná, můžeme použít jiné, složitější metody interpolací jako Natural neighbour interpolation, Weighted moving averages, Splines, nebo Kriging.
GRID-to-TIN konverzi můžeme považovat za speciální případ konverze bodů do TINu. GRID-to-TIN konverzi může být také považována za speciální případ generalizace TINU: redukuje se počet vrcholů TINu k reprezentaci terénu. GRID může být jednoduše triangulován do regulární trojúhelníkové sítě. V literatuře je popsáno mnoho algoritmů. Většina těchto metod má následující charakteristické vlastnosti: (1) výběr bodu GRIDu, který se ponechá nebo zruší, a (2) rozhodnout kdy zastavit vybírání a rušení bodů.
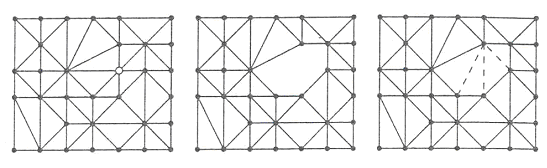
První metoda rozhoduje které body GRIDu ponechat nebo zrušit tím, že na začátku každému bodu přiřadí důležitost. Důležitosti je dosahnuto tak, že se porovná elevace bodu GRIDu s interpolovanou elevací – kde se povrch interpoluje z osmi sousedů zkoumaného bodu. Jsou ponechány pouze ty body GRIDu, kde je největší rozdíl. Tyto body mohou být triangulovány, např. Delaunyho triangulací a vzniknou vrcholy TINu. Viz. následující obrázek.
Druhá metoda (např. Lee´s drop heuristic) se liší od té předchozí tím, že se body ruší skokově, namísto použití předpočítané důležitosti.
Třetí metoda začíná s triangulací pouze ze čtyř rohových bodů GRIDu a stále zjemňuje trojúhelníkovou síť přidáváním dalších trojúhelníků. Zjemňování končí, když trojúhelníková síť dostatečně aproximuje povrch GRIDu.
Jiná metoda začíná detekováním specifických tvarů terénu GRIDu jako vrcholy, dolíky, sedlové body, hřebenice a údolnice. Poté se dokompletuje do formy TINu.
Konverze vrstevnic do TINu je velmi užitečná, protože výšková data jsou často získána digitalizováním vrstevnic z mapy. Samotná vrstevnicová mapa je již vlastně vektorová datová struktura, de facto rovinná projekce, kde vrcholy a linie mají přiřazenou výšku vrstevnice na které leží. K převedení vrstevnic do TINu se obvykle provede triangulace všech oblastí – což znamená triangulace „mezi“ vrstevnicemi. Každou oblast si můžeme představit jako polygon s dírami a nabízejí se standardní triangulační algoritmy známé a používané pro řešení tohoto problému ve výpočetní geometrii.
Místo použití těchto metod triangulace, použijeme tu, která vytváří pěkně tvarované trojúhelníky, jako je např. Delaunayho triangulace. Každopádně, na vstupu do triangulačního algoritmu je polygon a ne množina bodů. Existuje triangulace, která velmi přesně kopíruje Delaunayho triangulaci – musí být dána množina hran (vrstevnic), na kterých je provedena triangulace. Tato triangulace je nazývána Vázaná Delaunyho triangulace (Constrained Delaunay triangulation).
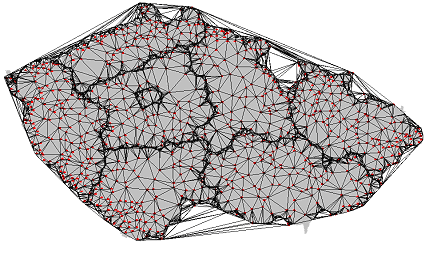
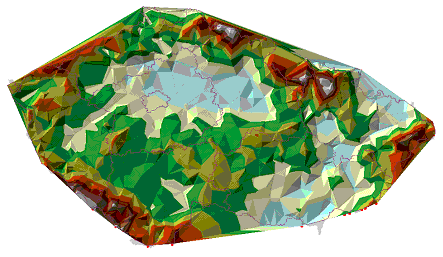
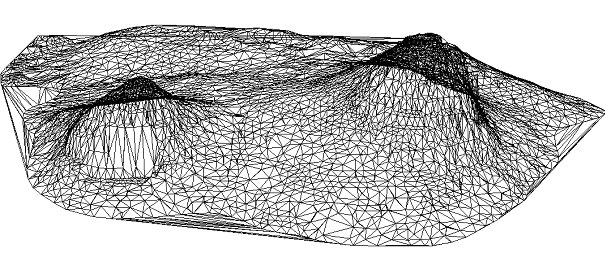
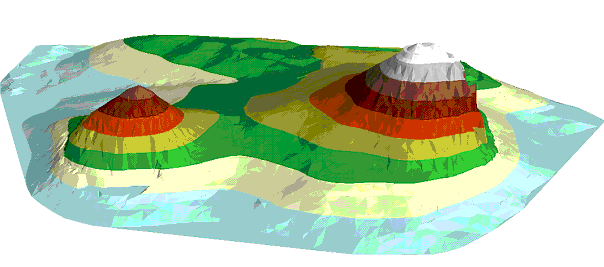
K dosažení nejlepších výsledků jakékoliv oblasti je dobré použít kombinaci lomových bodů a vrstevnic. Rozdíl mezi triangulací pouze z vrstevnic a touto „kombinovavnou“ triangulací je vidět na obrázcích níže. Je patrné, že „kombinovaná“ triangulace dává lepší výsledky na vrcholcích hor, kde vrstevnice nejsou dostatečně husté a triangulace vytváří na modelu terénu malé plošky.
Dále je patrné, že v místech bez vrstevnic jsou vytvořeny špatně tvarované trojúhelníky. Tato místa bez vrstevnic mohou vzniknout digitalizováním analogové mapy v místě skalních útvarů, které nejsou možné vyjádřit vrstevnicemi. Když do modelu přidáme lomové body – trojúhelníky aproximují terén velmi dobře a vytvořený model terénu je uspokojivý.
Literatura:
[Geographical Information Systems and Computer Cartography, Christopher B. Jones, Singapore; Algorithmic Foundations of Geographic Information Systems, Marc van Kreveld, Springer; Generalization in Digital Cartography, Robert B. McMaster, Washington; Predansky z predmetu KMA/UGI, Karel Jedlicka, Plzen]